A. Memahami hubungan garis dengan garis, garis dengan sudut, serta menentukan ukuranya.

1.) Garis yang melalui AB dan garis yang melalui DC adalah dua garis yang sejajar (tidak berpotongan). Mengapa? Coba carilah pasangan-pasangan garis lain yang sejajar! dan disebut segmen garis (segmen) AB dan DC. AB ≅ DC dibaca segmen AB kongruen (gambar geometri yang sama) dengan segmen DC.
Segmen AB dan segmen BA adalah segmen yang sama sehingga dapat ditulis AB = BA (karena keduanya merupakan himpunan titik-titik yang sama), sedangkan AB dan DC dan adalah segmen berbeda dan tidak dapat ditulis sebagai AB = DC . Carilah segmen lain yang sama.
2.) Garis yang melalui AB dan garis yang melalui AD adalah dua garis yang berpotongan. Mengapa? Coba carilah pasangan-pasangan garis lain yang berpotongan!. AB dan AD adalah dua segmen.
3.) Garis yang melalui AB dan FG adalah dua garis yang bersilangan (tidak sejajar dan juga tidak berpotongan). Mengapa? Coba carilah pasangan-pasangan garis lain yang bersilangan!
4. Untuk setiap tiga titik berbeda pada suatu garis, salah satu tiik terletak antara dua titik lainnya.
a. Tiga segmen berbeda: AB, AC , BC b.Tiga sinar berbeda: sinar AD, sinar DA, sinar BD c. Garis: garis AD, garis BC, garis BD
5.) Suatu segmen memiliki dua titik akhir dan dapat diukur panjangnya. Panjang segmen AB kita notasikan dengan AB = AB. Misalnya AB = AB = 3.
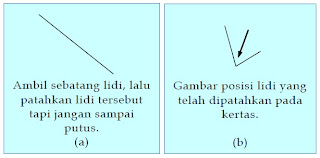
B.Pengertian Sudut
Gambar diatas merupakan salah satu contoh dari sudut. Dalam Matematika, sudut terbentuk dari dua sinar yang titik pangkalnya berimpit, seperti tampak pada gambar di bawah ini.
Berdasarkan Gambar di atas, maka bagian-bagian sudut terdiri dari dua buah kaki sudut, titik sudut, dan daerah sudut. Kaki sudut adalah sinar garis yang membentuk suatu sudut. Titik sudut adalah titik potong pangkal sinar dari kaki sudut. Daerah sudut yaitu daerah yang terbentuk antara dua kaki sudut. Sudut pada Gambar tersebut dinamakan dengan sudut ABC yang disimbolkan dengan ∠ABC atau sudut CBA yang disimbolkan dengan ∠CBA atau hanya ditulis sudut B yang disimbolkan dengan ∠B. C.Mengukur Ukuran Sudut dengan Busur Derajat
ada busur derajat terdapat dua deretan angka yaitu bagian atas dan bagian bawah. Pada bagian atas, dari kiri ke kanan tertulis angka 0, 10, 20, 30, . . . , 180, sedangkan di bagian bawah dari kiri ke kanan tertulis 180, 170, 160, . . . , 0. Perpotongan antara garis horizontal dengan garis vertikal disebut pusat busur. Untuk mengukur sudut PQR di atas caranya sebagai berikut.
1. Letakkan pusat busur derajat pada titik sudut, yaitu titik Q. Impitkan garis horisontal busur derajat yang tertulis angka 0 pada salah satu kaki sudut, yaitu QR.
2. Lihatlah angka pada busur derajat yang berimpit dengan kaki sudut yang lain, yaitu kaki sudut QP berimpit dengan garis yang menunjukkan angka 100. Jadi ukuran ∠PQR di atas adalah 100°.